" Le groupe de Puteaux et la « Section d'or » "

Par Jean Roussaux

          Il y a eu entre 1911 et 1914 un groupe d'artistes et de critiques apparentés au cubisme* qui se constitua à Puteaux autour des Frères Duchamp, en particulier du peintre Gaston Emile Duchamp dit jacques Villon qui s'était installé à Puteaux dès 1906. Ce groupe réunit d'abord, à cette époque, Albert Gleizes (plutôt courbevoisien d'ailleurs), Roger de La Fresnaye, Fernand Léger, Jean Metzinger, Francis Picabia, Henry Valensi et Frantisek Kupka. Un temps, Apollinaire et le critique américain Walter Pach participeront également à ce groupe auquel Villon donna nom de « Section d'or » parce que l'une de leurs préoccupations était d'ordre mathématique et reliée au nombre d'or ou section d'or. Autour de ce noyau, se regroupa une nébuleuse d'artistes cubistes tels Jeanne Rij-Rousseau, Henri le Fauconnier, Démétrios Galanis, Marie Laurencin, Paul Véra, Maurice Princet, le mathématicien du cubisme, Louis Marcoussis et bien d'autres.

*On peut situer la naissance du cubisme autour de 1907-1909 avec la formation de la première équipe cubiste avec Braque et Picasso mais aussi des peintres qui appartiendront au groupe de Puteaux comme Gleizes, Villon ou Kupka. On peut voir dans le groupe de Puteaux, qui s'est peut-être constitué en réaction au cubisme scientifique trop géométrique, l'expression d'un cubisme intellectuel et méthodique mais respectueux de la sensibilité esthétique et de la couleur.

          D'abord défini par Euclide puis développé par Platon, le nombre d'or ou section dorée ou encore divine proportion au sens du poème musical de Scriabine, est défini par (a+b) /a = a/b parfois représenté par Φ (Phi, en hommage au sculpteur Phidias). C'est la solution positive d'une équation du type X²-X-1= 0 qui vaut (1+5^1/2)/2 = 1,618.. Ce nombre d'or est une curiosité mathématique. Un rectangle d'or a pour longueur Φ et largeur l'unité. Si l'on retranche de cette surface un carré de côté un, la surface restante est encore celle d'un rectangle d'or et ainsi de suite. On passe d'un rectangle d'or au suivant en divisant ses dimensions par Φ. On obtient ainsi des rectangles de plus en plus petits dont le rapport des cotés est toujours de 1,618... On peut aussi définir un angle d'or, une spirale d'or et bien d'autres curiosités mathématiques autour de ce nombre irrationnel.

          Il y a bien longtemps que des mathématiciens, des architectes et des peintres se sont intéressés à la « section d'or ». Ainsi au 15ème siècle Paolo Uccello est préoccupé par des problèmes de perspective et l'intervention de point de fuite multiples dans certaines de ses œuvres destinés à représenter les corps dans l'espace. Piero Della Francesca aborde aussi des problèmes de géométrie dans son traité sur les corps réguliers et la perspective en peinture. Ces préoccupations géométriques les confrontent à la section d'or, supposée clé de l'harmonie céleste.

          En 1509, Luca Pacioli livre dans « la divine proportion », qu'illustre Léonard de Vinci, des raisons d'y trouver des attributs qui n'appartiennent qu'à Dieu. Ce nombre singulier n'est en effet pas sans rapport avec des relations naturelles qui caractérisent la morphologie des plantes et des animaux, voire des formations cristallines ou les spirales des nébuleuses galactiques. Ainsi Le nombre d'or se rencontre dans la suite de Fibonacci qui caractérise la phyllotaxie* chez certaines plantes, la spirale de certaines coquilles ou l'agencement pentagonal des atomes dans les mailles de quasi- cristaux.

*La phyllotaxie est le mode d'insertion des feuilles sur la tige. Il y a plusieurs types de phyllotaxies et pour chacune on peut définir un indice de phyllotaxie (A/B) qui tient compte du nombre de spires, nombre de tours de tige (A) et du nombre des entre noeuds (B) qui séparent deux feuilles occupant la même position sur la tige. Les indices les plus souvent observés se rangent dans une suite de Fibonacci (Mathématicien italien ayant introduit la notation arabe en arithmétique) : 1/1 ;1/2 ;1/3 ;2//5[(1+1) / (2+3)] ; 3/8[(2+1) / (5+3)] ;5/13 ;8/21 ;13/34, etc..Les angles de divergence (angle que forment les pétioles de deux feuilles consécutives) qui correspondent à ces indices ont pour mesure angulaire respectivement : 360 ;180 ;120 ;144 ;135 ;138,46 ;137,14 ;137,65 ;etc. degrés, valeurs qui sont de plus en plus proches de l'angle d'or (137°5)

          Comme depuis les origines on a voulu relier la beauté et l'harmonie à des données mathématiques, l'utilisation du nombre d'or expliquerait la perfection de certaines œuvres comme le Parthénon voire la pyramides de Khéops dont le quotient de l'arête sur le côté vaut approximativement le nombre d'or. On le rencontrerait aussi dans de nombreux tableaux : par exemple dans la naissance de Vénus (fig.1) de Botticelli, dans la célèbre Joconde (fig.2) ou chez le pointilliste Seurat (fig.3). Ces allégations ne sont pas sans susciter de nombreuses contestations. Pourtant depuis cette époque, certains artistes continuent à affirmer qu'il existerait une perfection dans les proportions qui serait à l'origine de la beauté et qui se révèlerait déjà dans la nature végétale ou minérale.

          Ces préoccupations mathématiques furent surtout développées au sein du groupe de Puteaux en particulier par Marcel Duchamp qui s'intéressait aussi à l'optique et à la mécanique. Mais les propos qui se tenaient dans les réunions de cet aréopage putéolien n'étaient pas que mathématiques et centrés sur les géométries non-euclidiennes ou la quatrième dimension mais aussi sur l'art africain, l'abstrait ou l'analyse de la décomposition du mouvement par les enregistrements chronophotographiques de Marey (qui sont certainement à l'origine du nu descendant un escalier (fig.4) de Duchamp). Il faut d'ailleurs remarquer que bien peu d'œuvres des artistes ayant appartenu à la nébuleuse « Section d'or » présentent des dimensions ou une structure faisant apparaitre la divine proportion*

*Le format d'un tableau de Gleizes, les Baigneuses, (1912) correspond à un rectangle d'or. En revanche, ni les œuvres de Villon ou de Duchamp, ni celles de beaucoup d'autres membres du groupe de Puteaux ne font apparaître la « section d'or » ; Ces artistes ne semblent d'ailleurs jamais avoir indiqué qu'ils y avaient fait appel.

          Plus tard, vers 1920, le groupe de Puteaux composé de nombreux artistes qui s'y rattachent s'intéresse au Dadaïsme et au Surréalisme, inaugurant ainsi des développements futurs. A partir de 1925 beaucoup de ces artistes trouveront un mécène en Camille Renault, le célèbre restaurateur du «Big-Boy»

          Après avoir en 1911 animé au salon des indépendants la salle 41 qui regroupait les œuvres cubistes d'Archipenko, de Delaunay, de Gleizes, de Duchamp, de Metzinger et de bien d'autres et scandalisé le salon d'automne, les peintres du groupe exposent dans la galerie de l'art contemporain, rue Tronchet. Le cubisme n'étant pas bien vu du salon d'automne, Villon démissionne du comité d'organisation dont il était membre depuis 1904 et il organise en octobre 1912 le 1er salon de la Section d'or dans la boutique d'un marchand de meubles rue La Boétie (Galerie La Boétie). Un critique, peu perspicace, doute alors que cette éphémère crise de géométrie plane ait un retentissement mondial. Bien d'autres expositions suivront à Paris, en province et à l'étranger auxquelles participeront des peintres et sculpteurs appartenant ou ayant appartenu à la nébuleuse putéolienne « Section d'or ».

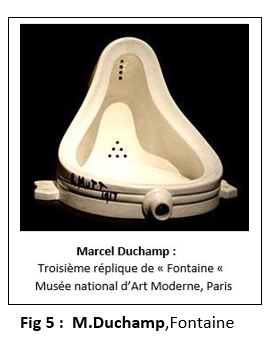
          C'est probablement Marcel Duchamp (1887- 1968) qui fut le plus prolixe en matière d'innovations, introduisant vers 1915 ses absurdes ready-made comme cette fontaine urinoir (fig.5) ou l'inverse. Il se partage entre la France et les Etats-Unis où il organisa des expositions d'art moderne. Bien sûr par la suite, beaucoup d'autres artistes peintres ou sculpteurs fréquenteront le « Cercle d'or » chez Villon. Mais ces réunions cessèrent, semble-t-il, à partir de 1925 avec la dernière exposition de la « Section d'or » à la Galerie Vavin-Raspail. Nombreux sont ceux qui par la suite s'inscriront dans la lignée de la « Section d'or », comme Macario Vitalis ou René Pradez. Mais ceux qui furent, tout au long de cette aventure, les plus fidèles à Puteaux sont Villon et Kupka.

          Pour un cubiste comme Villon (1875-1963), Il s'agit d'abord de l'abandon des formes arrondies et de la délicatesse du modelé au profit de grands plans et de la prédominance de la ligne droite. Villon développera dans ses œuvres un système de formes qu'il s'est inventé et qui n'est pas sans rappeler ce que Vinci appelait la vision pyramidale et que je baptiserais volontiers de majoritairement tétraédrique dans le cas, par exemple, de Vue de l'Hôtel de Ville, Jour de Marché (fig.6) œuvre d'un de ses disciples, car les diverses parties de l'objet nous seraient perceptibles sous la forme de tétraèdres dont l'un des sommets touche notre œil et la base découpe des triangles dans l'objet.

          Quant à Kupka (1871-1957), d'origine tchèque, un pionnier de l'abstraction, il se distingua par des œuvres où les couleurs l'emportent sur les soucis géométriques qui prédominent dans le cubisme. Il est le digne représentant de l'orphisme, cette tendance invoquée par Apollinaire pour désigner le cubisme coloré, mais sa création échappe d'emblée au répertoire cubiste(fig.7). Bien sûr d'autres peintres et sculpteurs fréquenteront l'atelier de Villon. A partir de 1925, certaines de leurs œuvres seront acquises par le restaurateur Camille Renault qui deviendra alors le mécène incontournable de ce groupe de Puteaux.

          Ainsi, par les œuvres de ces peintres et sculpteurs de la « Section d'or », Puteaux a acquis une place enviable dans la grande histoire de la peinture. Puisse leur souvenir entretenir chez de nombreux putéoliens le goût des arts plastiques.

J.R - 04/2021

Pour en savoir plus :

- Le groupe de Puteaux, Wikipédia, l'encyclopédie libre.
- La section d'or Wikipédia, l'encyclopédie libre.
- Cassou Jean : Panorama des Arts plastiques contemporains, Gallimard,1960.
- Corbalan Fernando : le nombre d'or dans le langage mathématique de la beauté, collection présentée
   par C.Villani (Institut Henri Pointcaré) 2013.
- Damoiseau Murielle : Camille Renault. Site de la SHALP-Puteaux.
- Durand Philippe : Mathématiques et botanique, nombre d'or, angle d'or, suite de Fibonacci
   et phyllotaxie, Carnets de Botanique. Société Occitane n°22,2020.
- Honour Hugh et Fleming John : Histoire mondiale de l'art, Bordas,1984.